Unleashing the Power of Genetic Algorithms: Theory and Hands-On Coding

Genetic Algorithm - Introduction

•       The genetic algorithm is a method for solving optimization problems that mimic some of the processes observed in natural evolution.

•       Genetic algorithms in particular became popular through the work of John Holland in the early 1970s, and particularly his book Adaptation in Natural and Artificial Systems (1975).

•       GA is based on ideas from Darwinian Evolution theory of “Survival of the fittest”.

•       The genetic algorithm repeatedly modifies a population of individual solutions.

•       At each step, the genetic algorithm selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. Over successive generations, the population "evolves" toward an optimal solution.

•       The genetic algorithm uses three main types of rules at each step to create the next generation from the current population:

•       Selection rules select the individuals, called parents, that contribute to the population at the next generation.

•       Crossover rules combine two parents to form children for the next generation.

•       Mutation rules apply random changes to individual parents to form children.

Biological Background

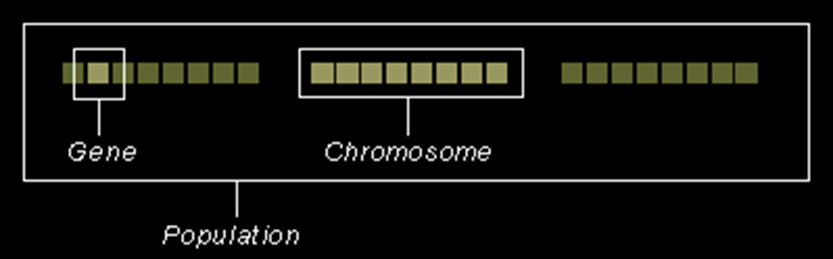
•       Each cell of a living organisms contains chromosomes - strings of DNA

•       Each chromosome contains a set of genes - blocks of DNA

•        A collection of genes – genotype

•        A collection of aspects (like eye colour) – phenotype

•        Reproduction involves recombination of genes from  parents.

•        The fitness of an organism is how much it can reproduce before it dies.

Search Space

•       A population of individuals are maintained within search space for a GA, each representing a possible solution to a given problem.

•       Each individual is coded as a finite length vector of components, or variables, in terms of some alphabet, usually the binary alphabet {0,1}.

•       To continue the genetic analogy, these individuals are likened to chromosomes and the variables are analogous to genes.

•       Thus, a chromosome (solution) is composed of several genes (variables).

•       A fitness score is assigned to each solution representing the abilities of an individual to `compete'.

•       The individual with the optimal (or generally near optimal) fitness score is sought.

•       The GA aims to use selective `breeding' of the solutions to produce `offspring' better than the parents by combining information from the chromosomes.

Implementation Details

After an initial population is randomly generated, the algorithm evolves the through three operators:

1. selection which equates to survival of the fittest;
2. crossover which represents mating between individuals;
3. mutation which introduces random modifications.

Selection Operator

•       key idea: give preference to better individuals, allowing them to pass on their genes to the next generation.

•       The goodness of each individual depends on its fitness.

•       Fitness may be determined by an objective function or by a subjective judgement.

Crossover Operator

•       Two individuals are chosen from the population using the selection operator.

•       A crossover site along the bit strings is randomly chosen.

•       The values of the two strings are exchanged up to this point.

•       If S1=000000 and S2=111111 and the crossover point is 2 then S1'=110000 and S2'=001111.

•       The two new offspring created from this mating are put into the next generation of the population.

•       By recombining portions of good individuals, this process is likely to create even better individuals.

Mutation Operator

•       With some low probability, a portion of the new individuals will have some of their bits flipped.

•       Its purpose is to maintain diversity within the population and inhibit premature convergence.

•       Mutation alone induces a random walk through the search space.

•       Mutation and selection (without crossover) create a parallel, noise-tolerant, hill-climbing algorithms.

Termination

•       This generational process is repeated until a termination condition has been reached. Common terminating conditions are:

•       A solution is found that satisfies minimum criteria.

•       Fixed number of generations reached.

•       Allocated budget (computation time/money) reached.

•       The highest-ranking solution's fitness is reaching or has reached a plateau such that successive iterations no longer produce better results.

•       Manual inspection Combinations of the above.

Figure 1: Flow Chart of GA

Pseudo-Code

A generalized pseudo-code for a GA is explained in the following program −

GA()

initialize population

find fitness of population

while (termination criteria is reached) do

parent selection crossover with probability pc

mutation with probability pm

decode and fitness calculation

survivor selection

find best

return best

A Genetic Algorithm Example

•       As a simple example, imagine a population of four strings, each with five bits.

•       Also imagine an objective function f(x)=2x.

•       The goal is to optimize (in this case maximize) the objective function over the domain 0 ≤

$x\le 31.$

•       Now imagine a population of the four strings in Table 1, generated at random before GA execution.

•       The corresponding fitness values and percentages come from the objective function f(x).

Table 1 Four strings and their fitness values

• The values in the 

$$\frac{f_i}{\sum f_i}$$column provide the probability of each string's selection.

•       So initially 11000 has a 38.1% chance of selection, 00101 has an 7.9% chance, and so on.

•       The results of the selections are given in the “Actual Count” column of Table 1.

•       As expected, these values are similar to those in the “Expected Count” column.

•       After selecting the strings, the GA randomly pairs the newly selected members and looks at each pair individually.

•       For each pair (e.g. A = 11000 and B = 10110), the GA decides whether or not to perform crossover.

•       If it does not, then both strings in the pair are placed into the population with possible mutations (described later).

•       If it does, then a random crossover point is selected, and crossover proceeds as follows: A = 1 1 | 0 0 0

•          B = 1 0 | 1 1 0

•       are crossed and become A' = 1 1 1 1 0        B' = 1 0 0 0 0.

•       Then the children A' and B' are placed in the population with possible mutations.

•       The GA invokes the mutation operator on the new bit strings very rarely (usually on the order of ≤0.01 probability), generating a random number for each bit and flipping that particular bit only if the random number is less than or equal to the mutation probability.

•       After the current generation's selections, crossovers, and mutations are complete, the new strings are placed in a new population representing the next generation, as shown in Table 2.

•       In this example generation, average fitness increased by approximately 30% and maximum fitness increased by 25%.

•       This simple process would continue for several generations until a stopping criterion is met.

Table 2 The population after selection and crossover

Applications

Automotive design

•       In designing composite materials and aerodynamic shapes for race cars and regular means of transportation (including aviation) can return combinations of best materials and best engineering to provide faster, lighter, more fuel efficient and safer vehicles.

•       The process can be done much quicker and more efficiently by computer modelling using GA searches to return a range of options for human designers.

Engineering design

•       To optimize the structural and operational design of buildings, factories, machines, etc. is a rapidly expanding application of Gas.

•        Used to optimizing the design of heat exchangers, robot gripping arms, satellite booms, building trusses, flywheels, turbines, and just about any other computer-assisted engineering design application.

Robotics

•       Robotics involves human designers and engineers trying out all sorts of things in order to create useful machines that can do work for humans.

•       GAs can be programmed to search for a range of optimal designs and components for each specific use, or to return results for entirely new types of robots that can perform multiple tasks and have more general application.

Optimized Telecommunications Routing

•       GAs are being developed that it will allow for dynamic and anticipatory routing of circuits for telecommunications networks.

•       These could take notice of your system's instability and anticipate your re-routing needs.

•       Optimize placement and routing of cell towers for best coverage and ease of switching.

Trip, Traffic and Shipment Routing

•       Traveling Salesman Problem or TSP can be used to plan the most efficient routes and scheduling for travel planners, traffic routers and even shipping companies.

•       The shortest routes for traveling and the  timing to avoid traffic tie-ups and rush hours.

•       GA contributed more to it than the  travel agent did.

•       Computer Gaming

•       Encryption and Code Breaking

•       Computer Aided Molecular Design 

•       Gene Expression Profiling

•       Finance and Investment strategies

•       Marketing and Merchandising

Python Implementation

Below is a Python implementation of a genetic algorithm to maximize the objective function $f(x) = 2x$ for binary strings of length 5, representing numbers in the range $0 \leq x \leq 31$. Four initial strings will be used as the starting population.

import random

def binary_to_decimal(binary_str):

    """Convert a binary string to a decimal integer."""

    return int(binary_str, 2)

def decimal_to_binary(decimal_num, length=5):

    """Convert a decimal integer to a binary string of a given length."""

    return format(decimal_num, f'0{length}b')

def objective_function(x):

    """Objective function to maximize."""

    return 2 * x

def fitness(binary_str):

    """Calculate the fitness of a binary string based on the objective function."""

    x = binary_to_decimal(binary_str)

    return objective_function(x)

def select_parents(population):

    """Select two parents using a roulette wheel selection."""

    fitness_scores = [fitness(individual) for individual in population]

    # print(fitness_scores)

    total_fitness = sum(fitness_scores)

    probabilities = [score / total_fitness for score in fitness_scores]

    # print(probabilities)

    return random.choices(population, weights=probabilities, k=2)

def crossover(parent1, parent2):

    # print('parents:',parent1,parent2)

    """Perform single-point crossover between two parents."""

    point = random.randint(1, len(parent1) - 1)

    child1 = parent1[:point] + parent2[point:]

    # print(child1)

    child2 = parent2[:point] + parent1[point:]

    # print(child2)

    return child1, child2

def mutate(individual, mutation_rate=0.1):

    """Mutate an individual with a given mutation rate."""

    # print(individual)

    individual = list(individual)

    for i in range(len(individual)):

        if random.random() < mutation_rate:

            individual[i] = '1' if individual[i] == '0' else '0'

    # print(''.join(individual))

    return ''.join(individual)

def genetic_algorithm(population, generations, mutation_rate=0.1):

    """Run the genetic algorithm."""

    for generation in range(generations):

        new_population = []

        for _ in range(len(population) // 2):

            parent1, parent2 = select_parents(population)

            child1, child2 = crossover(parent1, parent2)

            child1 = mutate(child1, mutation_rate)

            child2 = mutate(child2, mutation_rate)

            new_population.extend([child1, child2])

        population = new_population

        # Debugging: print the best individual in the current generation

        best_individual = max(population, key=fitness)

        print(f"Generation {generation + 1}: Best Individual = {best_individual}, Fitness = {fitness(best_individual)}")

    return max(population, key=fitness)

# Initial population: four random 5-bit strings

population = [decimal_to_binary(random.randint(0, 31)) for _ in range(4)]

# print(population)

# Run the genetic algorithm

generations = 10

mutation_rate = 0.1

best_solution = genetic_algorithm(population, generations, mutation_rate)

# Output the best solution

best_x = binary_to_decimal(best_solution)

print(f"Optimal solution: x = {best_x}, f(x) = {objective_function(best_x)}")

Explanation:

1. Initialization:

   • The population consists of 4 random binary strings, each 5 bits long.

2. Fitness Function:

   • The fitness is calculated as $f(x) = 2x$, where $x$ is the decimal value of the binary string.

3. Selection:

   • Roulette wheel selection is used to choose parents based on their fitness.

4. Crossover:

   • A single-point crossover is performed to generate offspring.

5. Mutation:

   • Each bit in the offspring has a small probability (mutation rate) of flipping.

6. Iteration:

   • The algorithm runs for a specified number of generations, maintaining a population size of 4.

7. Output:

   • The binary string and its corresponding decimal value with the highest fitness are returned as the optimal solution.

This implementation includes debug output to track the best individual in each generation.